निर्देश: एक संस्थान में 800 छात्र हैं। छात्र संस्थान जाने और वापस आने के लिए परिवहन के विभिन्न साधनों का उपयोग करते हैं। दिया गया पाई आरेख अपेक्षित डेटा को दर्शाता है। आरेख का ध्यानपूर्वक अध्ययन करें और प्रश्नों के उत्तर दें।

यदि वर्ष के दौरान सरकार द्वारा खर्च की गई कुल राशि ₹3,00,000 करोड़ थी, तो राज्य के विकास पर खर्च की गई राशि खेलों पर खर्च की गई राशि से कितनी अधिक है?

ABCD एक चक्रीय चतुर्भुज है। AB और DC जब बढ़ाई जाती है, तो वे P पर मिलती है,  यदि PA = 8 cm है, PB = 6 cm है, PC = 4 cm है, तो PD की लंबाई कितनी है?

एक त्रिभुज का आधार 16 cm है और इसका क्षेत्रफल $${144cm^2}$$ है। दिए गए आधार के संबंध में इसकी संगत ऊंचाई ज्ञात कीजिए।

यदि (m + 1) = √n + 3, तो $${1\over 2}\left({m^3-6m^2+12m-8\over \sqrt { n}}-n \right)  \ $$ का मान है

△ABC, B पर समकोण त्रिभुज है और tan A = $$3\over 4$$, तो sin A + sin B + sin C इसके बराबर होगा:

cos 120⁰ का सटीक मान ज्ञात कीजिए।

X एक काम को 25 दिनों में खत्म कर सकता है। उसी काम को Y, 20 दिनों में कर सकता है। दोनों मिलकर 5 दिनों तक काम करते हैं और फिर X चला जाता है। अकेले Y कितने दिनों में शेष काम को पूरा करता है?

निर्देश: ग्राफ को पढ़ें और निम्नलिखित प्रश्नों के उत्तर दें।

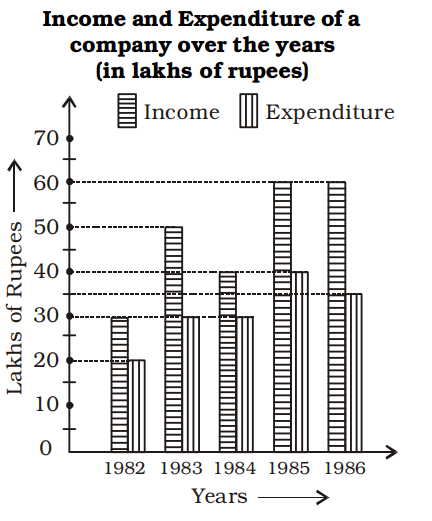
1983 और 1984 के लाभ में कितना अंतर है (लाख रुपये में)?