- टेस्ट सीरीज और प्रैक्टिस टेस्ट
- समय साबित परीक्षा रणनीतियों
- परीक्षा विश्लेषण और नकली परीक्षण
- Hand-on वास्तविक समय परीक्षण अनुभव

हाल ही में जोड़े गए पोस्ट और देखें >>
मिरर इमेज रीज़निंग प्रश्न प्रतिस्पर्धी परीक्षाओं में पाई जाने वाली एक सामान्य प्रकार की समस्या है, विशेष रूप से विश्लेषणात्मक और स्थानिक तर्क कौशल का आकलन करने वाले परीक्षणों में। इन मिरर इमेज रीजनिंग प्रश्नों में, उम्मीदवारों को एक आकृति, पैटर्न या व्यवस्था प्रस्तुत की जाती है,
रीज़निंग क्विज़ प्रश्न और उत्तर किसी व्यक्ति की तार्किक सोच, समस्या को सुलझाने के कौशल और जानकारी का विश्लेषण करने की क्षमता का परीक्षण और मूल्यांकन करने के लिए डिज़ाइन किए गए हैं। इन प्रश्नोत्तरी में आम तौर पर प्रश्नों की एक श्रृंखला शामिल होती है जिसमें प्रतिभागियों को सही उत्तर पर पहुंचने के लिए तर्क और कटौती लागू करने की आवश्यकता होती है।
रीज़निंग क्विज़ प्रश्नों को किसी व्यक्ति की तार्किक रूप से सोचने, जानकारी का विश्लेषण करने और दिए गए परिसरों के आधार पर निष्कर्ष निकालने की क्षमता का परीक्षण करने के लिए डिज़ाइन किया गया है। इन रीज़निंग क्विज़ प्रश्नों का उद्देश्य किसी व्यक्ति के महत्वपूर्ण सोच कौशल और समस्याओं को प्रभावी ढंग से हल करने की उनकी क्षमता का आकलन करना है।
उत्तर के साथ एक गैर-मौखिक तर्क परीक्षण एक आकलन है जो किसी व्यक्ति की भाषा और मौखिक संचार पर भरोसा करने के बजाय दृश्य और स्थानिक कौशल का उपयोग करके समस्याओं का विश्लेषण और समाधान करने की क्षमता को मापता है।
वर्तमान में होने वाली प्रतियोगी परीक्षाओं में एक - एक अंक का महत्व इसना बढ़ गया हैं कि एक अंक हमें हजारों विद्यार्थीओ से आगे खड़ा कर देता हैं। इसी बात को मध्य नज़र रखते हुए Examsbook ने प्रतियोगी परीक्षाओं के लिये MCQ प्रश्नो के साथ नॉन-वर्बल रीजनिंग का ब्लॉक तैयार किया है।
गैर-मौखिक तर्क भाषा या शब्दों पर भरोसा किए बिना दृश्य जानकारी को समझने और उसका विश्लेषण करने की क्षमता है। इस प्रकार के तर्क में समस्याओं को हल करने और जानकारी को समझने के लिए छवियों, आरेखों, प्रतीकों और पैटर्न का उपयोग करना शामिल है।
प्रचारक की क्षमता और चॉप का आकलन करने के लिए उत्तर के साथ तर्कपूर्ण प्रश्न और उत्तर, कई कंपनियां, सरकारी संघ और विभिन्न सार्वजनिक और राज्य की स्थिति वाले विश्वविद्यालय तर्क के आधार पर प्रतियोगी परीक्षा या चयन परीक्षा आयोजित कर रहे हैं।
SSC Stenographer की जरूरत हर सरकारी विभाग में बनी रहती है। इस वजह से यह एक बहुत ही लोकप्रिय काम होता जा रहा है। यदि आप एसएससी स्टेनो की तैयारी कर रहे हैं तो आपको यहां दिए गए प्रश्नों का अभ्यास अवश्य करना चाहिए। इन प्रश्नों को परीक्षा के सिलेबस को ध्यान में रखकर तैयार किया गया है।
सबसे लोकप्रिय पोस्ट
सबसे लोकप्रिय पोस्ट
हाल ही में जोड़े गए प्रश्न
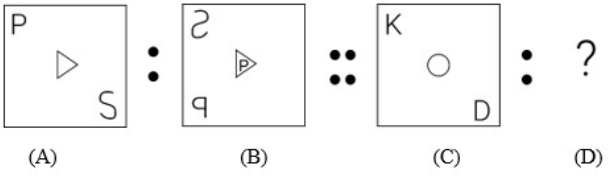
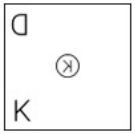
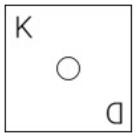
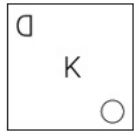
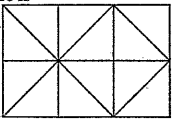
आकृति A एक निश्चित पैटर्न के अनुसार B से संबंधित है। उसी पैटर्न का अनुसरण करते हुए आकृति C, D से संबंधित है। पैटर्न का अध्ययन करें और उस आकृति का चयन करें, जिसे D के स्थान पर रखा जाना चाहिए।
- 1false
- 2true
- 3false
- 4false
- उत्तर देखेंउत्तर छिपाएं
- Workspace
- SingleChoice
उत्तर : 2 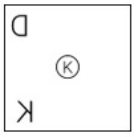
- 17false
- 28false
- 39true
- 410false
- उत्तर देखेंउत्तर छिपाएं
- Workspace
- SingleChoice
उत्तर : 3 9
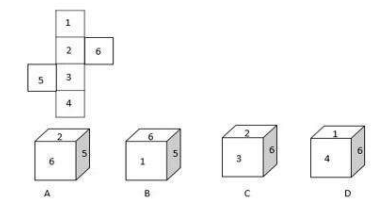
उस घन का चयन करें जो दी गई शीट को रेखाओं के अनुदिश मोड़कर बनाया जा सकता है।
- 1केवल Dfalse
- 2केवल A और Cfalse
- 3केवल C और Dtrue
- 4केवल Bfalse
- उत्तर देखेंउत्तर छिपाएं
- Workspace
- SingleChoice
उत्तर : 3 केवल C और D
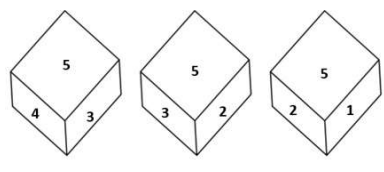
एक ही पासे की तीन अलग-अलग स्थितियां दिखाई गई हैं। संख्या '5' दर्शाने वाले फलक के विपरीत फलक पर कौनसी संख्या होगी।
- 12false
- 21false
- 36true
- 43false
- उत्तर देखेंउत्तर छिपाएं
- Workspace
- SingleChoice
उत्तर : 3 6
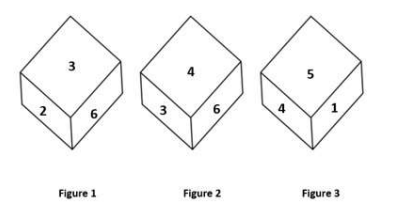
एक ही पासे की तीन अलग-अलग स्थितियां दिखाई गई हैं। संख्या '2' को दर्शाने वाले फलक के विपरीत फलक पर संख्या होगी?
- 14true
- 26false
- 35false
- 41false
- उत्तर देखेंउत्तर छिपाएं
- Workspace
- SingleChoice