जितना ब्याज 5 वर्ष में 4% की साधारण ब्याज दर पर ₹6,000 का होगा उतना ब्याज ₹8,000 की राशि पर 3% प्रति वर्ष की दर पर कितने समय में होगा?

27 वस्तुओं का क्रय मूल्य 18 वस्तुओं के विक्रय मूल्य के बराबर है। लाभ प्रतिशत कितना है?

यदि $$ cosecθ + cotθ =p $$ है, तो $${p^2-1}\over{p^2+1}$$  का मान है:

निर्देश: यहां दी गई तालिका वर्ष 1989 से 1994 तक एक कंपनी द्वारा पांच प्रकार की कारों का उत्पादन दर्शाती है। तालिका का अध्ययन करें और प्रश्नों के उत्तर दें।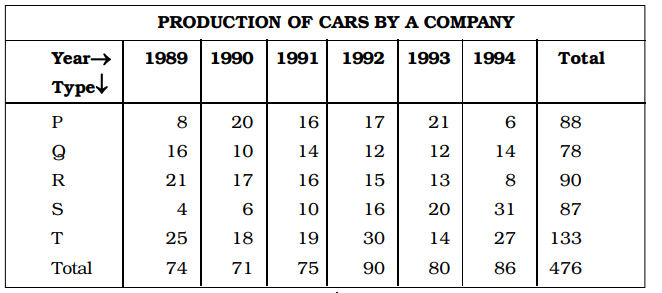

1992 में सभी प्रकार की कारों के कुल उत्पादन में 1991 की तुलना में कितने प्रतिशत की वृद्धि हुई:

एक वस्तु का अंकित मूल्य उसके लागत मूल्य से 40% अधिक है। यदि इसका विक्रय मूल्य अंकित मूल्य का $$73{1\अधिक 2}\%$$ है, तो लाभ प्रतिशत है

यदि 2x² – 7x + 5 =0, तो $$x^2+{25\over 4x^2}$$ का मान क्या है

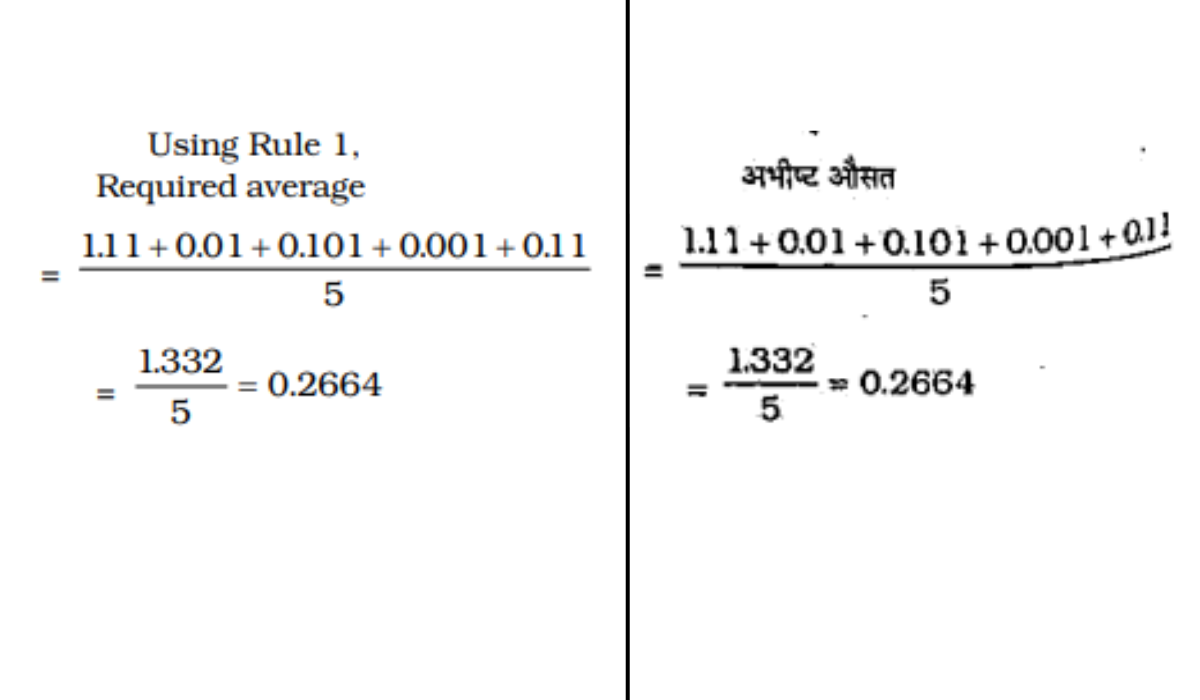
1.11, 0.01, 0.101, 0.001, 0.11 का औसत ज्ञात कीजिए

निर्देश: प्रश्नों के उत्तर देने के लिए निम्नलिखित बार ग्राफ का ध्यानपूर्वक अध्ययन करें।

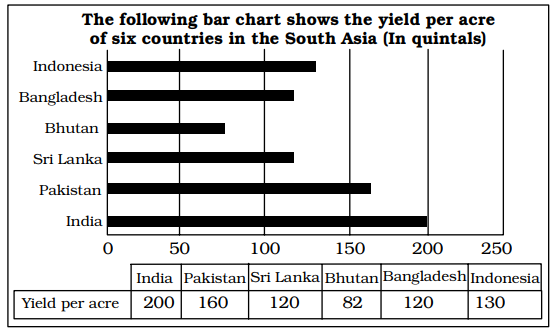
भारत की प्रति एकड़ उपज पाकिस्तान की तुलना में कितने प्रतिशत अधिक है?