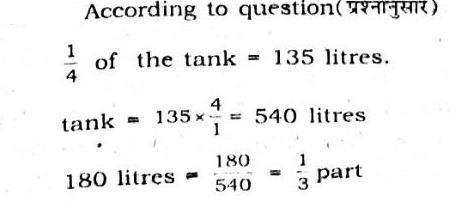Pipes and Cisterns प्रश्न और उत्तर का अभ्यास करें
5 प्र: एक टैंक से दो इनलेट A और B जुड़े हुए हैं। A और B क्रमशः 32 घंटे और 28 घंटे में टैंक भर सकते हैं। यदि दोनों पाइपों को A से शुरू करके 1 घंटे के लिए बारी-बारी से खोला जाता है, तो टैंक कितने समय में (निकटतम पूर्णांक तक घंटों में) भर जाएगा?
1745 064abe4c38c254a4ceae3718d
64abe4c38c254a4ceae3718d- 122false
- 230true
- 336false
- 424false
- उत्तर देखेंउत्तर छिपाएं
- Workspace
- SingleChoice
उत्तर : 2. "30"
प्र: पाइप A और B एक टैंक को क्रमशः 43.2 मिनट और 108 मिनट में भर सकते हैं। पाइप C इसे 3 लीटर/मिनट की दर से खाली कर सकता है। जब तीनों पाइप एक साथ खोले जाते हैं, तो वे टंकी को 54 मिनट में भर देते हैं। टैंक की क्षमता (लीटर में) है:
1453 064be670e23047f4c71dc9c2d
64be670e23047f4c71dc9c2d- 1200false
- 2160false
- 3180false
- 4216true
- उत्तर देखेंउत्तर छिपाएं
- Workspace
- SingleChoice
उत्तर : 4. "216"
प्र: पाइप A और B एक टैंक को क्रमशः 12 मिनट और 15 मिनट में भर सकते हैं। टैंक भरा होने पर पाइप C द्वारा x मिनट में खाली किया जा सकता है। जब तीनों पाइप एक साथ खोले जाते हैं, तो टंकी 10 मिनट में भर जाती है। x का मान है:
1159 064d20e2de0ce557496830b4f
64d20e2de0ce557496830b4f- 118false
- 215false
- 320true
- 424false
- उत्तर देखेंउत्तर छिपाएं
- Workspace
- SingleChoice
उत्तर : 3. "20"
प्र: एक टैंक को A द्वारा 60 मिनट में भरा जा सकता है और B द्वारा 75 मिनट में खाली किया जा सकता है। टैंक आधा भरा हुआ है और रवि टैंक भरना चाहता है लेकिन गलती से B खोल देता है और उसे आधे घंटे के बाद पता चलता है और नल B बंद कर दिया है। फिर वह A खोलता है और टैंक _______ मिनट में पूरी तरह भर जाता है।
1089 064e75543de1aa1b70fdef7a0
64e75543de1aa1b70fdef7a0- 148false
- 254true
- 350false
- 464false
- 5इनमें से कोई नहींfalse
- उत्तर देखेंउत्तर छिपाएं
- Workspace
- SingleChoice
उत्तर : 2. "54"
प्र: एक टैंक के एक-चौथाई हिस्से में 135 लीटर पानी है। यदि टंकी में 180 लीटर पानी है तो टंकी का कौन सा भाग भरा हुआ है?
1066 0650832b16e0e55b91dcd1a53
650832b16e0e55b91dcd1a53- 1$$1\over 3$$true
- 2$$1\over 6$$false
- 3$$2\over 5$$false
- 4$$2\over 3$$false
- उत्तर देखेंउत्तर छिपाएं
- Workspace
- SingleChoice
उत्तर : 1. "$$1\over 3$$"
व्याख्या :