Trigonometry प्रश्न और उत्तर का अभ्यास करें
8 4 प्र:
5f589a1f2025ff52f0526ecf 4 प्र:
5f4df2b17e85226ee745ec9c 4 प्र:
5f4df246081699374e855fcf 4 प्र:
5f4df1da5e74bc4ee553cec8 4 प्र:
5f4df136081699374e8550a6 4 प्र:
5f40dfa24c9a9415f7cdfc3b 4 प्र:
5f40dcdcb8958f14fa2b34f6 4 प्र:
5f3f941f9b782961da39057a
प्र: यदि sin3θ=cos(20° - θ) है तो θ का मान होगा।
1368 05f589a1f2025ff52f0526ecf
5f589a1f2025ff52f0526ecf- 140°false
- 235°true
- 360°false
- 430°false
- उत्तर देखेंउत्तर छिपाएं
- Workspace
- SingleChoice
उत्तर : 2. "35°"
प्र: यदि x+ y=90°, है तो $$ {\sqrt{cosx.cosecy-cosx.siny}}$$ का मान क्या होगा?
1082 05f4df2b17e85226ee745ec9c
5f4df2b17e85226ee745ec9c- 1cosxfalse
- 2sinxtrue
- 3$$ {\sqrt{sinx}}$$false
- 4$$ {\sqrt{cosx}}$$false
- उत्तर देखेंउत्तर छिपाएं
- Workspace
- SingleChoice
उत्तर : 2. "sinx"
प्र: यदि tan A=n tan B और Sin A= m Sin B, है तो Cos2A का मान होगा।
1136 05f4df246081699374e855fcf
5f4df246081699374e855fcf- 1$$ {m^{2}+1\over {n^{2}+1}}$$false
- 2$$ {m^{2}+1\over {n^{2}-1}}$$false
- 3$$ {m^{2}-1\over {n^{2}-1}}$$true
- 4$$ {m^{2}-1\over {n^{2}+1}}$$false
- उत्तर देखेंउत्तर छिपाएं
- Workspace
- SingleChoice
उत्तर : 3. "$$ {m^{2}-1\over {n^{2}-1}}$$"
प्र: sin222° + Sin268°+ Cot2 30° का मान होगा।
1084 05f4df1da5e74bc4ee553cec8
5f4df1da5e74bc4ee553cec8- 1$$ {5\over 4}$$false
- 2$$ {3\over 4}$$false
- 34true
- 43false
- उत्तर देखेंउत्तर छिपाएं
- Workspace
- SingleChoice
उत्तर : 3. "4"
प्र: दिये गये चित्र में BC=15 cm , Sin B=4/5 है तो AB का मान होगा।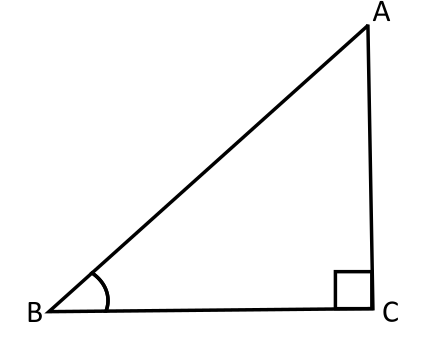
1320 05f4df136081699374e8550a6
5f4df136081699374e8550a6
- 125 सेमीtrue
- 220 सेमीfalse
- 35 सेमीfalse
- 44 सेमीfalse
- उत्तर देखेंउत्तर छिपाएं
- Workspace
- SingleChoice
उत्तर : 1. "25 सेमी"
प्र: यदि $$ {1+sinθ\over {1-sinθ}}={p^{2}\over{q^{2}}}$$, है तो sec θ का मान होगा।
1142 05f40dfa24c9a9415f7cdfc3b
5f40dfa24c9a9415f7cdfc3b- 1$$ {2p^{2}{q^{2}}\over {p^{2}+{q^{2}}}}$$false
- 2$${1\over 2}\left({q\over p}+{p\over q} \right)$$true
- 3$$ {1\over {p^{2}}}+{1\over {q^{2}}}$$false
- 4$$ {p^{2}q^{2}}\over{p^{2}+q^{2}}$$false
- उत्तर देखेंउत्तर छिपाएं
- Workspace
- SingleChoice
उत्तर : 2. "$${1\over 2}\left({q\over p}+{p\over q} \right)$$"
प्र: $$ {25 cosec^{2}θ +25sin^{2}θ}$$ का न्यूनतम मान होगा?
1211 05f40dcdcb8958f14fa2b34f6
5f40dcdcb8958f14fa2b34f6- 125false
- 250true
- 355false
- 420false
- उत्तर देखेंउत्तर छिपाएं
- Workspace
- SingleChoice
उत्तर : 2. "50"
प्र: $${cos^2A\over {1+sinA}}$$ का मान क्या होगा?
1002 05f3f941f9b782961da39057a
5f3f941f9b782961da39057a- 11+sinAfalse
- 21-sinAtrue
- 31+secAfalse
- 41-secAfalse
- उत्तर देखेंउत्तर छिपाएं
- Workspace
- SingleChoice
उत्तर : 2. "1-sinA"
hn16814

