Clock Reasoning Trick and Formula in Hindi

रीजनिंग सेक्शन में, हर प्रतियोगी परीक्षा में घड़ी के टॉपिक से जुड़ें प्रश्न शामिल होते हैं। साथ ही फॉर्मूला, प्रश्नों को जल्दी हल करने में मदद करता है लेकिन आपको केवल यह सीखने की आवश्यकता है कि समस्या को हल करने के लिए ट्रिक के साथ किसी भी सूत्र का उपयोग कैसे किया जाए। इसलिए, यहां मैं रीजनिंग में प्रश्नों को हल करने के लिए सूत्रों के साथ घड़ी के प्रश्नों से संबंधित बुनियादी अवधारणाओं और ट्रिक्स को शेयर कर रहा हूं। ये ट्रिक्स और फॉर्मूले आपाकी आगामी प्रतियोगी परीक्षाओं में निश्चित रूप से आपकी मदद करेंगे। आपको अपने प्रदर्शन को सुधारने के लिए इन ट्रिक्स, फ़ार्मुलों और उदाहरणों के साथ अभ्यास करना चाहिए।

Tricks and Formula of Clock Reasoning in Hindi

घड़ी क्या है ? 

घड़ी एक इलेक्ट्रॉनिक उपकरण जिसका उपयोग समय को दर्शाने और बनाए रखने के लिए किया जाता है। इसमें तीन सुइयां होती है सबसे बड़ी सुई सेकंड को, मध्य वाली मिनट को तथा सबसे छोटी सुई घंटे को दर्शाती है | यह सुईया अलग - अलग समय में अपना एक चक्कर पूरा करती है |

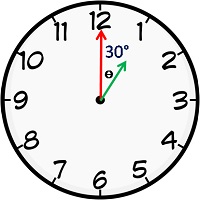
घड़ी में कुल 12 भाग होते है अर्थात 12 घंटे होते है | प्रत्येक 1 घंटे में 30⁰ का कोण बनता है तथा 12 घंटो में 360⁰ का कोण बनता है | इसे इस प्रकार भी लिख सकते है

12 घंटो में कोण बनते है = 360⁰

तो 1 घंटो कोण बनेगा = 360⁰/12 = 30⁰

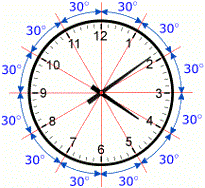
इस प्रकार घडी के एक भाग से दूसरे भाग तक जाने में प्रत्येक सुई 30⁰ का कोण बनाती है | परन्तु इस दुरी को तय करने में अलग-अलग समय लेती है |

घडी से सम्बंधित महत्वपूर्ण नियम: 

घंटे वाली सुई -

60 मिनट में कोण बनाती है = 360⁰

1 मिनट में कोण बनेगा = 360⁰/60⁰ = 6⁰

मिनट वाली सुई

5 मिनट में कोण बनाती है = 30⁰

1 मिनट में कोण बनेगा =  30⁰/5 =6⁰

सेकंड वाली सुई

60 सेकंड में कोण बनाती है = 360⁰

1 सेकंड में कोण बनेगा =  360⁰/60 = 6⁰

घंटे व मिनट की सुइयों के मध्य 1 मिनट में तय दुरी –

मिनट वाली सुई 60 मिनट में 60 मिनट की दुरी तय करती है जबकि घंटे वाली सुई 60 मिनट में 5 मिनट की दुरी तय करती है इस प्रकार 60 मिनट में मिनट वाली सुई, घंटे की सुई से 55 मिनट की अधिक दुरी तय करती है |  

⸫ 55 मिनट की दुरी तय करती है 60 मिनट में

⸫ 1 मिनट की दुरी तय करेगी = 60/55 मि. या 12/11 मि. में 

उदारहण. किसी घडी में 4 बजकर 40 मिनट हो रहे है तो बताओ घडी की दोनों सुइयों के मध्य कितने डिग्री का कोण होगा | 

(A) 100⁰

(B) 80⁰

(C) 120⁰

(D) 200⁰

हल 

शोर्ट ट्रिक : 

1 भाग = 30० 

तो 4 भाग = 30×4 = 120० 

परन्तु घंटे वाली सुई अपने भाग में 40 मिनट की दुरी पहले ही तय कर चुकी है तो 40 मिनट में बना कोण = 

अब दोनों सुईयो के मध्य बना कोण = 120० – 20० = 100० 

फार्मूला : 

कोण निकालना =  $${11× min-60×time \ given \over2} $$

   $${11×40-60×4  \over2} $$

   $${200  \over2} = 100^0 $$

दर्पण-प्रतिबिम्ब ट्रिक :  

दर्पण प्रतिबिम्ब में दायीं स्थिति बांयी ओर तथा बायीं स्थिति दायीं ओर प्रतीत होती है 

उदारहण: किसी घडी में 3 बजकर 35 मिनट हो रहे है यदि इसे दर्पण में देखंगे तो कितना समय प्रतीत होगा ?

हल 

जब वास्तविक समय देकर, प्रतिबिम्ब समय पूछे या प्रतिबिम्ब समय देकर वास्तविक समय पुछे तो दिए गए समय को 11 : 60 में से घटा देंगे 

11 : 60 – 3 : 35 = 8 : 25

नोट:- दिया गया समय 11 : 00 से अधिक दिया परन्तु 1 : 00 से कम हो तो ऐसी अवस्था में उसे 23 : 60 में से घटना अधिक सुविधा जनक रहेगा | 

जल प्रतिबिम्ब ट्रिक:

जल प्रतिबिम्ब में ऊपर की अवस्था निचे की ओर तथा निचे के अवस्था ऊपर की ओर पलट जाती है | 

नोट : यदि दिया गया समय 1-6  तक का है तो उसे 6.30 में से घटायेंगे | यदि दिया गया समय 7-1 तक का है तो उसे 18.30 में से घटायेंगे |

उदारहण : एक घडी में केवल 3,6,9 और 12 के स्थान पर बिंदु लगे है उस घडी को दर्पण के सामने उल्टा रखा गया है एक व्यक्ति को घडी के प्रतिबिम्ब में 7.50 जैसा समय दिखाई दे रहा है तो घडी में वास्तविक समय क्या है ?

(A) 8.40

(B) 9.40

(C) 7.40

(D) 10.40

हल : 

वास्तविक समय = 18.30 – 7.50 = 10.40

घड़ी की सुईया आपस में एक-दूसरे के साथ तीन प्रकार से सम्बन्ध बनाती है 

(1) अतिव्यापन, एक ही सीध में या आच्छादित( 360⁰ या 0⁰ ) के कोण पर - जब मिनट वाली सुई घंटे वाली सुई के ऊपर हो तो ऐसी अवस्था अतिव्यापन कहलाती है |

● घडी की दोनों सुइयाँ 1 घंटे में 1 बार तथा 12 घंटे में 11 बार अतिव्यापित होती है | क्योकि 11-12 व 12-1 के बीच केवल 1 बार ही (12.00 बजे ) अतिव्यापित होती है | 

● घडी के दोनों सुइया 1 दिन में 22 बार अतिव्यापित होती है यहाँ एक दिन तात्पर्य ( दिन - रात) अर्थात 24 घंटो से है |

समय निकालना = बजकर 

उदारहण:  5 बजे से 6 बजे के बीच घडी की दोनों सुईया कितने बजे एक ही सीधे में होगी |

$$ (A) \ 5: 27{3\over11} $$

$$ (B) \ 5: 30{2\over11} $$

$$ (C) \ 5: 27{5\over11} $$

$$ (D) \ 5: 28{2\over11} $$

हल: 

$$  \ = {60\over11}×Given \ Time = {60\over11}×5   $$

  $$   \ = {300\over11} = 27{3\over11}$$

अर्थात   $$  \ 5: 27{3\over11} min $$

(2) विपरीत दिशा ( 180० के कोण पर ) – जब घडी की दोनों सुईयां विपरीत दिशा में हो तो 

● घडी की दोनों सुइया 1 घंटे में 1 बार तथा 12 घंटे में 11 बार विपरीत दिशा में होती है क्योकी 5-6 व 6-7 के बीच केवल 1 बार (6.00 बजे) विपरीत दिशा में होती है | 

घडी की दोनों सुइया 1 दिन में 22 बार विपरीत होती है | 

समय निकालना = बजकर 

(+) जब समय 6 से कम हो 

(-) जब समय 6 या 6 से अधिक हो 

उदारहण: 8 से 9 बजे के बीच घडी की दोनों सुइयों कितने बजे विपरीत दिशा में होगी | 

$$ (A) \ 8: 1{10\over11} min $$

 $$ (B) \ 8: 10{5\over11} min $$

  $$ (C) \ 8: 10{10\over11} min $$

  $$ (D) \ 8: 10{1\over11} min $$

हल :

$$  \ = {60\over11}×(8-6)= {60\over11}×2 $$

  $$   \ = {120^0\over11} = 10{10\over11}$$

अर्थात   $$  \ 8: 10{10\over11} min $$

(3) लम्बवत  (90⁰ के कोण पर),  समकोण पर - जब घडी की दोनों सुईया के मध्य 90⁰ का कोण बन रहा तो 

● घडी की दोनों सुईया 1 घंटे में 2 बार तथा 12 घंटे में 22 बार लम्बवत  होती है 

क्योकि 2-3 व 3-4 के बीच 4 बार नहीं 3 बार तथा 8-9 व 9-10 के बीच भी 4 बार नहीं 3 बार लम्बवत होती है इसलिए 2 बार की कमी हो जाती है |

● घडी की दोनों सुइया 1 दिन में 44 बार लम्बवत होती है |

समय निकालना = बजकर 

यहा (+) व (-) का चिन्ह दोनों उपयोग में लें हैं क्योकि दो बार लम्बवत होती है | 

उदारहण: 7 से 8 बजे के बीच कितने बजे दोनों सुइया लम्बवत होंगी |

  $$ (A) \ 7: 21{9\over11} min $$

  $$ (B) \ 7: 53{6\over11} min $$

  $$ (C) \ 7: 20{8\over11} min $$

  $$ (D) \ 7: 50{3\over11} min $$

हल: 

समय= 

$$  \ = {60\over11}×(7+3)= {60\over11}×10 $$

  $$   \ = {600\over11} = 54{6\over11}$$

अर्थात   $$  \ 7: 54{6\over11} min $$

समय  $$  \ = {60\over11}×(7-3)= {60\over11}×4 $$

   $$   \ = {240\over11} = 21{9\over11}$$

अर्थात   $$  \ 7: 21{9\over11} min $$

● जब घडी की दोनों सुइया आपस में अपना स्थान अदल-बदल करती है तो उनकी दुरी 60/13 के गुनज में होगी क्योकि दोनों सुइयों में अनुपात 60 : 5 या 12 : 1 होगा तो दोनों सुइयों के मध्य की दुरी =    $$  \ = {60\over12+1} = {60\over13}$$

उदारहण: सीता प्रात: 8 से 9 बजे के बीच विधालय गई | और सांय 5 से 6 बजे के बीच वापिस लौटी तो उसने देखा की सुइया की स्थिति वही है जो प्रातः थी | तो बताओ सीता कितने बजे विद्यालय गई थी |

हल: 

जाने का समय = × ( लौटने का बाद वाला) 

$$  \ = {60\over13}×6= {360\over13}= 27{9\over13}  $$

  अर्थात   $$  \ 8: 27{9\over13} min $$ पर गयी | 

लौटने का समय = × ( जाने का बाद वाला) 

$$  \ = {60\over13}×9= {540\over13}= 41{7\over13}  $$

  अर्थात   $$  \ 5: 41{7\over13} min $$

अभ्यास प्रश्न:

Q :  

7 और 8 बजे के बीच समय घडी की सुईया एक सीध में होगी लेकिन एक साथ नहीं होगी?

(A) 7 बजकर 5 मिनट पर

(B) 7 बजकर $$5{2\over 11} $$ मिनट पर

(C) 7 बजकर $$5{3\over 11} $$ $$ मिनट पर

(D) 7 बजकर $$5{5\over 11} $$ मिनट पर

(A) 6 O’ clock

(B) 03 : 45

(C) 12 O’clock

(D) 12 : 30

(A) 30°

(B) 45°

(C) 60°

(D) 90°

(A) 3 : 17

(B) 2 : 17

(C) 3 : 23

(D) 2 : 13

(A) 5 बजकर 40 मिनट पर

(B) 5 बजकर 45 मिनट पर

(C) 5 बजकर $$43{5\over 11} $$ मिनट पर

(D) 5 बजकर $$43{7\over 11} $$ मिनट पर

(A) पूर्व

(B) उत्तर-पश्चिम

(C) पश्चिम

(D) दक्षिण-पूर्व

(A) 08 : 10

(B) 01 : 40

(C) 04 : 50

(D) 10 : 20

(A) $$120^0$$

(B) $$3^0$$

(C) $$ \left( {3\over 10} \right)^0$$

(D) $$ \left( {10\over 3} \right)^0$$

(A) 4 : 35 am

(B) 4 : 39 am

(C) 4 : 40 am

(D) 4 : 38 am

(A) 12

(B) 22

(C) $${33\over 2} $$

(D) 15

मुझसे कमेंट बॉक्स में पूछें, अगर आपको घड़ी के एप्टीट्यूड प्रश्नों को हल करने में कोई समस्या आती है। अधिक घड़ी की समस्याओं के लिए अगले पेज पर जाएं।